圈住小猫游戏技巧攻略分享

圈住小猫游戏技巧攻略分享

　　这款游戏看似简单，但是实际操作起来发现并不如想象的那么简单，小便我已经玩了几十次了，依旧不能把这只猫给圈住。

　　在网上查了一下，原来这个游戏是有技巧的。现在分享出来，大家可以试一下，我已经将这只“神经猫”圈住好几次了!

　　定理1：

　　如果你在猫边上2格之内布子，除非有很好的地形，不然猫必定从你身边跑掉。所以在开阔场地，你的棋子至少和猫中间隔2个空格。

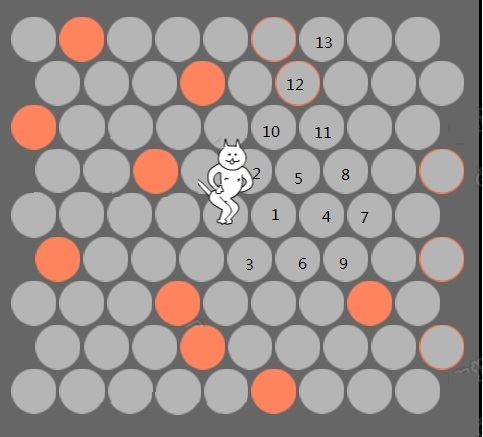
　　以此图为例：

　　设猫的目标是向右上开阔地逃跑。如果你走1，猫向右上走2，你再走5，猫走10……显然完全拦不住，猫直接往右上方跑走了。

　　如果你在4布点，猫还是向2移动，你走5的话和刚才一样了，走10的话猫走5，等等，还是不行。

　　但是如果在7布点，就不一样了。猫1，你8，猫5，你11，就拦在了猫前面，逼迫它转向，然后继续隔空下子。如果猫2，你可以13，等等，同样可以拦住。以此类推，在2步或更远以外的距离下子，在棋盘够大的情况下有很大概率挡住……但是棋盘可能不够大，见下。

　　定理2：

　　当你在开阔场地布下第一子时，封锁线会形成于你的这个子和猫中线的靠你那一侧。你应当让盘上已有子力和你的新子位于这条线上。

　　假设猫只能往右上逃而不能往左下跑。

　　红色方块代表猫的起始点，绿色六边形代表你的开局第一子。红色数字代表猫需要那么多步才能跑过去，绿色数字代表你的子需要那么多步才能连过去。

　　显然，如果某个格子上红字小于等于绿字，表明猫会比你先到，那么朝那里布防就是没有意义的，会被突破。想象一下你的棋子是在追猫的狗。

　　而蓝线标记的，就是刚好红字大于绿字的那条线。

　　所以你在布子的时候不要太激进，和猫靠的太近会被绕过去。要尽可能在封锁线的我方一侧布子，远远地形成包围之势。

　　定理3：猫是“贪心”的，所以你的布子方位要挡在猫的前方。

　　好吧虽然大部分人已经这么做了，但可能还是要说一下……

　　有些人想耍小聪明，不堵前方而堵后面，寄希望于猫犯蠢。根据我们的观察，这是没有必要的，猫的走法是“贪心法”——当前局势下，哪一步最有助于它逃脱，它就走哪一步。注意是当前局势，它不会玩佯攻，不会有长远考虑，所以其实是可以预判的。

　　而且利用这个特点，还可以给猫下陷阱：留一个开口，任猫向那里逃跑，同时加固别的防线;在最后一刻把那里封死。

　　猜想1：在足够大的棋盘上玩家有必胜策略。

　　之所以会有这个猜想，是因为博弈论里有一个问题，叫做“天使问题”(Angel problem)或者“天使与魔鬼”游戏。这是约翰·康威提出来的，就是那个生命游戏的康威。

　　在天使问题里，棋盘不是六边，而是标准的围棋盘;猫(天使)分级，一阶天使可以向3*3范围(周围8格内)没有魔鬼存在的任何一格移动，二阶天使可以向5*5范围内任何一格移动，等等。魔鬼可以向任何一个没有天使的格子里布子，有限步困住天使则魔鬼胜，天使无限存活下去则天使胜。

　　现在我们已经证明了：

　　二阶以上天使是有必胜策略的

　　一阶天使在32*33或者更小的棋盘上会输，否则也有必胜策略

　　如果天使的纵坐标永远不减少，或者距离原点的距离永远增加，那么会输

　　但是我还没有看到六边棋盘上的情况。考虑到猫的自由度比一阶天使还要小(只能走6格)，我打赌，哪怕盘上一个初始子没有，玩家也有必胜策略，但是我不知道这需要多大的棋盘。