杨辉三角的规律公式 杨辉三角java代码怎么写？

杨辉三角的基本特征

    杨辉三角就是两个未知数和的幂次方运算后的系数问题，比如（x+y）的平方=x的平方+2xy+y的平方，这样系数就是1,2,1这就是杨辉三角的其中一行，立方，四次方，运算的结果看看各项的系数，你就明白其中的道理了。杨辉三角最本质的特征是，它的两条斜边都是由数字1组成的，而其余的数则是等于它肩上的两个数之和。 

杨辉三角定律的来源

   中国古代数学家在数学的许多重要领域中处于遥遥领先的地位。中国古代数学史曾经有自己光辉灿烂的篇章，而杨辉三角的发现就是十分精彩的一页。 

    杨辉，字谦光，北宋时期杭州人。在他1261年所著的《详解九章算法》一书中，辑录了如上所示的三角形数表，称之为“开方作法本源”。 而这样一个三角在我们的奥数竞赛中也是经常用到，最简单的就是叫你找规律。

    北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算，南宋数学家杨辉在《详解九章算法》（1961年）记载并保存了“贾宪三角”，故称杨辉三角。元朝数学家朱世杰在《四元玉鉴》（1303年）扩充了“贾宪三角”成“古法七乘方图”。

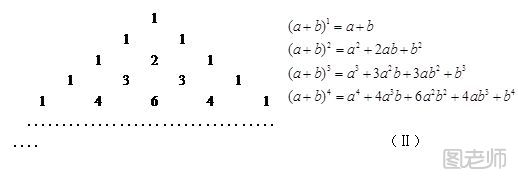
杨辉三角的Java代码

解法一

#include <stdio.h>

main()

{ int i,j,n=0,a[17][17]={0};

while(n<1 || n>16)

{ printf("请输入杨辉三角形的行数:");

scanf("%d",&n);

}

for(i=0;i<n;i++)

a[i][0]=1; /*第一列全置为一*/

for(i=1;i<n;i++)

for(j=1;j<=i;j++)

a[i][j]=a[i-1][j-1]+a[i-1][j];/*每个数是上面两数之和*/

for(i=0;i<n;i++) /*输出杨辉三角*/

{ for(j=0;j<=i;j++)

printf("%5d",a[i][j]);

printf("n");

}

}

点评：解法一是一般最容易想到的解法，各部分功能独立，程序浅显易懂。

解法二

#include <stdio.h>

main()

{ int i,j,n=0,a[17][17]={1};

while(n<1 || n>16)

{ printf("请输入杨辉三角形的行数:");

scanf("%d",&n);

}

for(i=1;i<n;i++)

{ a[i][0]=1; /*第一列全置为一*/

for(j=1;j<=i;j++)

a[i][j]=a[i-1][j-1]+a[i-1][j]; /*每个数是上面两数之和*/

}

for(i=0;i<n;i++) /*输出杨辉三角*/

{ for(j=0;j<=i;j++)

printf("%5d",a[i][j]);

printf("n");

}

}

点评：解窢二是在解法一的基础上，把第一列置为1的命令移到下面的双重循环中，减少了一个循环。注意初始化数组的变化。

解法三

#include <stdio.h>

main()

{ int i,j,n=0,a[17][17]={0,1};

while(n<1 || n>16)

{ printf("请输入杨辉三角形的行数:");

scanf("%d",&n);

}

for(i=1;i<=n;i++)

for(j=1;j<=i;j++)

a[i][j]=a[i-1][j-1]+a[i-1][j]; /*每个数是上面两数之和*/

for(i=1;i<=n;i++) /*输出杨辉三角*/

{ for(j=1;j<=i;j++) printf("%5d",a[i][j]);

printf("n");

}

}

点评：解法三是在解法一、二的基础上，把第一列置为1的命令去掉了，注意初始化数组的变化。

解法四

#include <stdio.h>

main()

{ int i,j,n=0,a[17][17]={0,1};

while(n<1 || n>16)

{ printf("请输入杨辉三角形的行数:");

scanf("%d",&n);

}

for(i=1;i<=n;i++)

{ for(j=1;j<=i;j++)

{ a[i][j]=a[i-1][j-1]+a[i-1][j]; /*每个数是上面两数之和*/

printf("%5d",a[i][j]); /*输出杨辉三角*/

}

printf("n");

}

}

点评：解法四是在解法三的基础上，把计算和打印合并在一个双重循环中。

相关链接：Java入门(13) More Java!